Optimization basic for ML
- 수학에서의 최적화 : 제약조건이 존재 할수도있는 상황에서 주어진 함수의 최대,최소점을 찾는 것.
Optimization in ML
- Training set 에 따라 정해지는 target function을 최저점을 만드는 model parameters를 찾는 것
- 보통 SGD(stochastic gradient descent)를 사용을 한다.
- loss function의 미분을 통해 error backpropagation algorithm사용.(chain rule)
Parameters Space Navigation
- ML 훈련가정 == 목적함수 최적화를 위한 매개변수 공간탐색
- 적정한 학습 모델(가설) 선택
- 목적함수 정의
- 학습 모델의 매개 변수 공간을 탐색하여 최저가 되는 최적점을 찾기.
- 특징 공간 보다 수 만배 많은 차원 을가진다.
ex) MINIST
- 28by28 의 image = 784차원의 특징 공간을 가지고
- 매개변수 공간은 수십만~수백만 차원의 매개 변수 공간을 가진다.
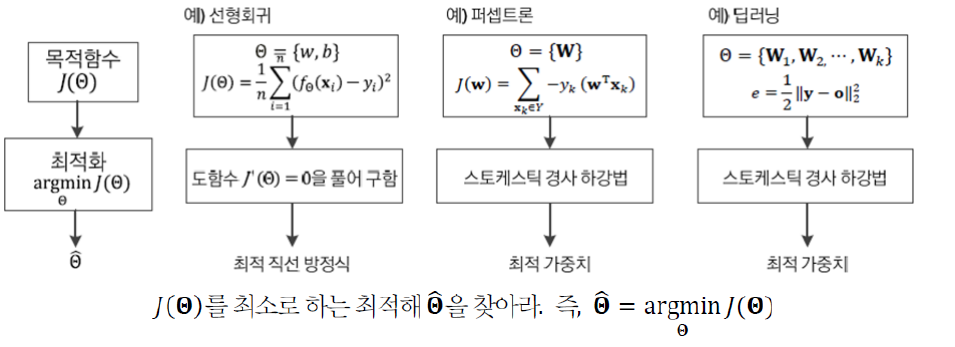
- 그리고 우리는 global minia를 찾고 있지만 local minia를 찾고 만족하는 경우가 많다. ex)
Jacobian matrix : 특정 행렬을 미분해서 얻은 행렬 Hessian matrix : 2차 미분 행렬
ML Optimization Strategy
- exhaustive search(낱낱탐색) Algorithm
- 모든 경우의 수를 보는 알고리즘
- 차원이 조금만 높아져도 적용이 불가능하다
- random search(무작위 탐색) Algorithm
- 전략없이 무작위로 탐색하는 순진한 알고리즘
- 램덤성으로 낱낱탐색보다 빠를수도 있다.
gradient descent(경사하강법) Algorithm
- 초기에 파라미터를 설정을 한다.
- 그리고 목점함수가 작아지는 방향으로 파라미터를 구함
파라미터가 작아지는 방향 : 미분값으로 계산
- 핵심원리 : \(d \theta = - f^`(x)\)
- gradient : 미분 값이 이루는 벡터
- ML 에서의 편미분 : 매개변수 집합은 복수 매개변수 이므로 편미분을 사용한다.
- learning rate: 탑색을할때 이동거리를 조절하는 역할
- \(\theta = \theta - pg\) : 위와같은 방법으로 gradient를 구한뒤 기울기가 낮은쪽으로 learning rate 만큼 이동하는걸 반복하여 최소값에 도달한다 .
- full- batch : 한번에 갱신
- 정확한 방향으로 수렴
- 하지만 느리다.
batch gradient descent
- sample 의 gradient를 구래 평균을 구한뒤 한꺼번에 update한다.
- training set 전체를 다 봐야지 update가 일어나므로 학습이 오래건린다.
SGD (stochastic gradient descent)
- mini-batch gradient descent 라고도 한다.
- mini-batch(one-smaple)의 gradient를 계산후 update.(나눠서 갱신)
- 수렴이 다소 해맬수 있다.
- 대신 빠르다.
- epoch : training set 한번을 다보고 학습을 시킨걸 1-epoch라고 한다.
- epoch 를 반복하여 학습.
Reference
- 기계학습(오일석)
- 이재구(인공지능/2022)(국민대)
